Adaptive Mesh Refinement for CFD Using Machine Learning
* This post shows some of the research I presented in AIAA SciTech 2021 and SciTech 2022.
Computational Fluid Dynamics (CFD) is a powerful tool for simulating and analyzing fluid flows, but it comes with a significant computational cost. One way to optimize this cost is through Adaptive Mesh Refinement (AMR), which dynamically increases mesh resolution in areas of interest while keeping it coarse elsewhere. However, traditional AMR methods often rely on user expertise and problem-specific knowledge. In this article, I will discuss a novel approach for automating the adaptive mesh refinement process using machine learning-based classifiers. I call it Smart AMR. The study performed here utilizes OpenFOAM CFD solvers and meshing framework that is coupled with TensorFlow ML framework for training/predictions.
What is Smart AMR?
Smart AMR combines classical adaptive mesh refinement techniques with machine learning to address some of the known issues in conventional approaches. The key innovation is the use of artificial neural networks (ANNs) and convolutional neural networks (CNNs) to make refinement decisions, reducing the reliance on user-defined criteria and potentially improving the generalizability of the dynamic mesh refinement process. In this post, an ANN classifier is discussed.
Feature Extraction for Classifier Training
Several normalized quantities such as velocity gradient, Q-criterion, vorticity, and a modified Δ criterion are used to capture flow features across different problems. The ability of such quantities in extracting refinement zones is evident in Figure 1.
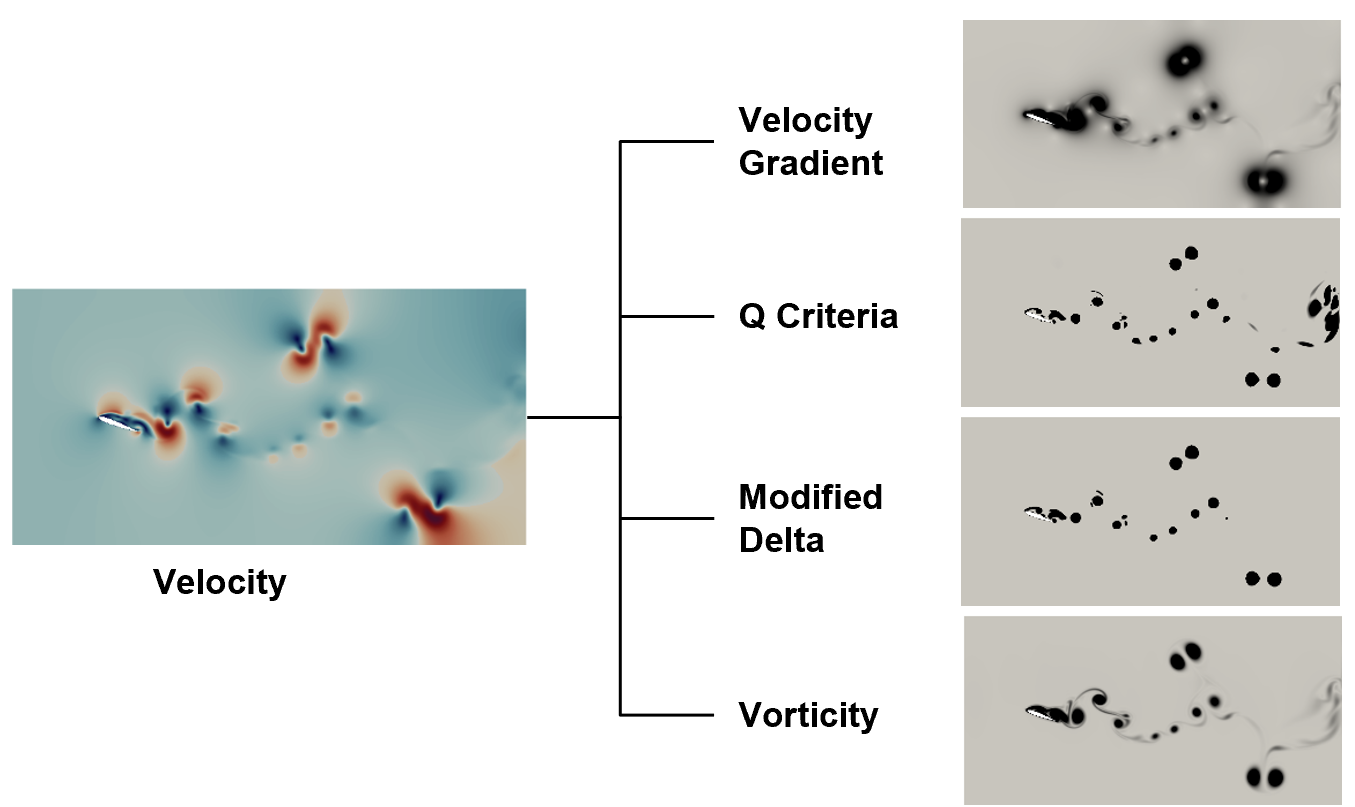
Training Data
Features extracted from several instantaneous velocity snapshots of the flow problems shown in Figure 2 were manually analyzed to generate a labeled training dataset where for each cell, a "to refine" or "not to refine" label was generated against 4 normalized (non-dimensional) input quantities. By training on data from multiple flow problems, the generalizability of the trained model can be improved.
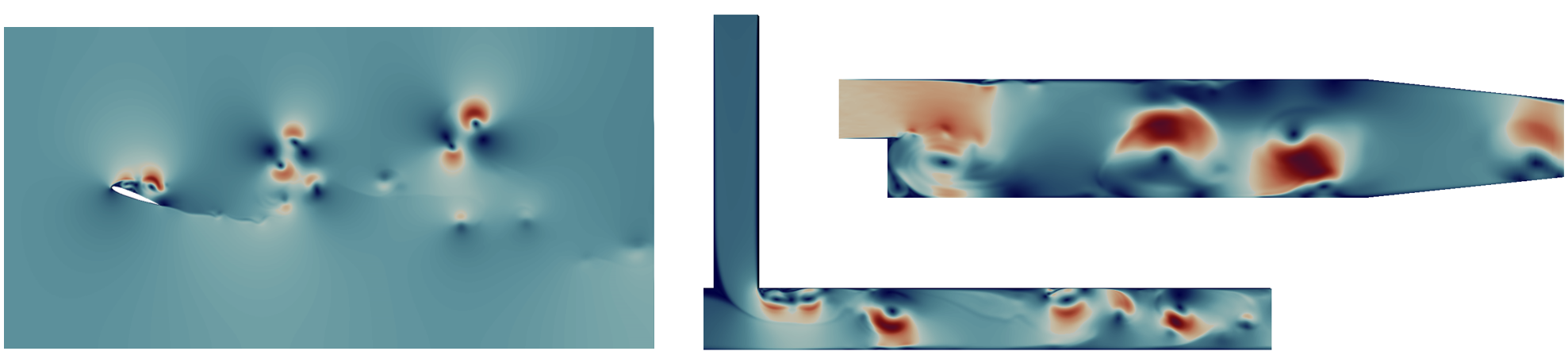
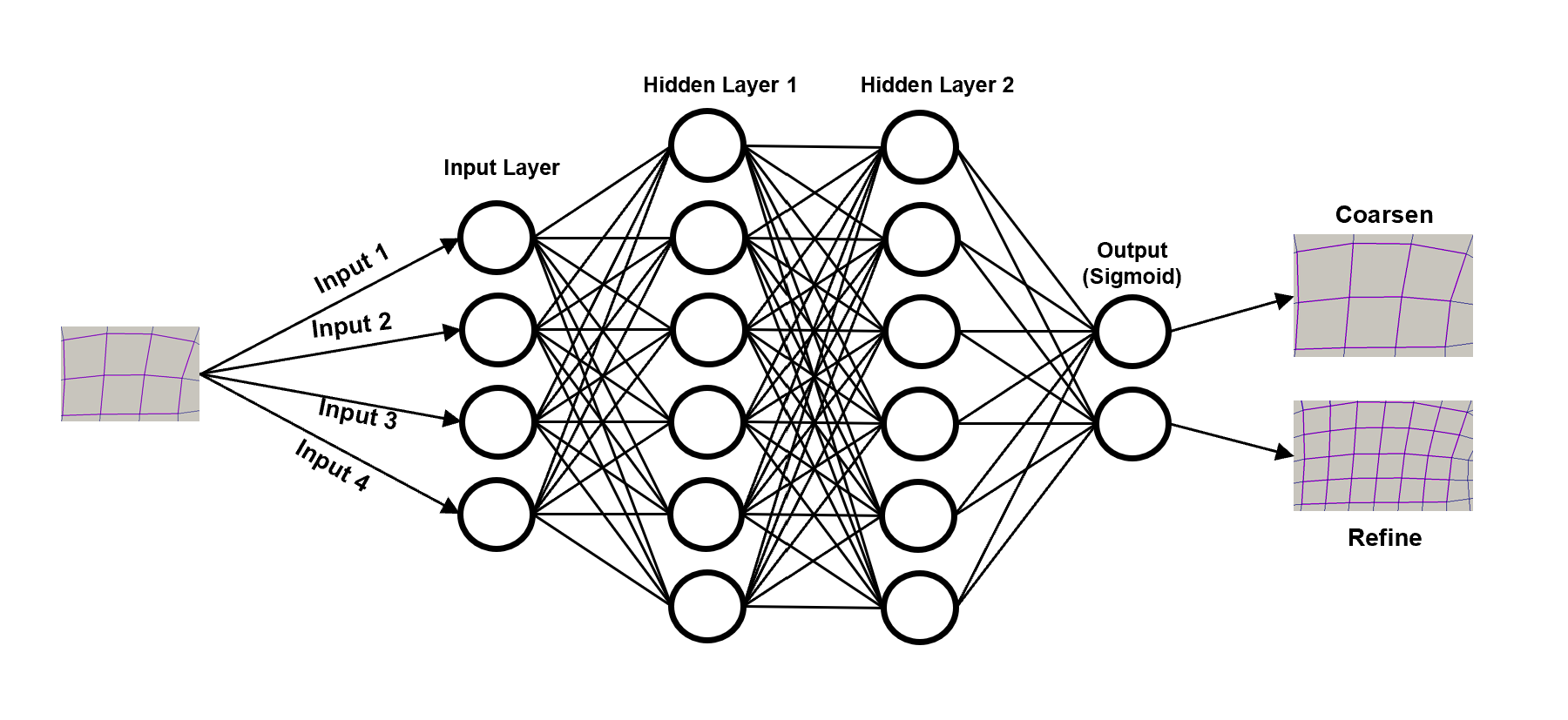
Artificial Neural Network (ANN) Architecture
ANNs work on the universal approximation theorem. Theoretically, ANNs can fit any non-linear data given enough parameters/layers. As shown in Figure 3, the ANN-based classifier has 4 inputs, several hidden layers, and one binary output. Inputs are the selected non-dimensional quantities computed on each cell, and output is the decision of "to refine" or "not to refine" for each cell.
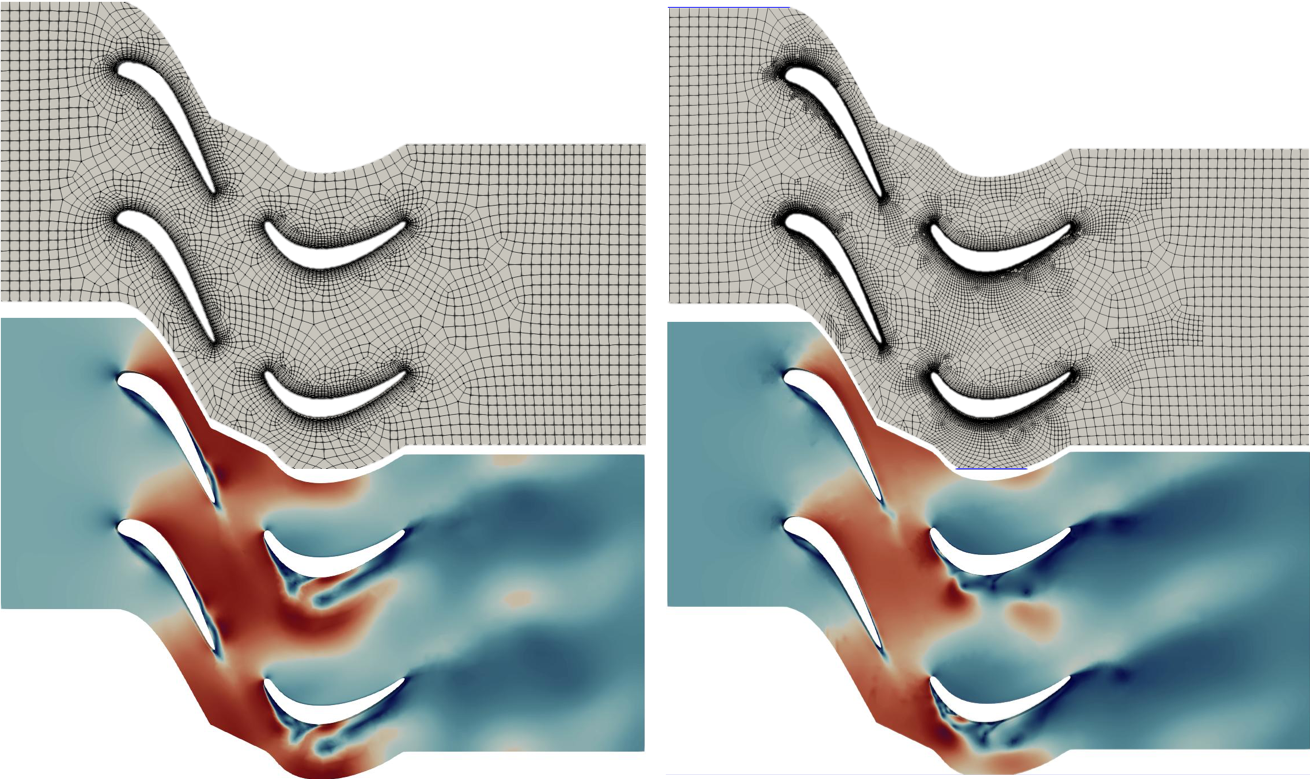
Promising Results
This Smart AMR approach is tested on a turbofan engine blade simulation which was not part of the training data. The results are encouraging:
- For the turbofan engine blade case, the classifier is able to correctly identify refinement zones as shown in Figure 4.
- This ANN-based classifier showed improved generalization, achieving 94% accuracy across different flow problems.
Implications and Future Work
Smart AMR has the potential to significantly improve the efficiency and accessibility of CFD simulations. By reducing the need for expert knowledge in mesh refinement, it could make high-quality CFD analysis more widely available. Additionally, the ability to generalize across similar problems could save substantial time in setting up new simulations.
Looking forward, this work can be extended to other physical phenomena beyond fluid dynamics and to three-dimensional cases. More complex network architectures can be explored to improve the robustness and generalizability of Smart AMR.
Conclusion
Smart Adaptive Mesh Refinement represents a promising step forward in the intersection of machine learning and computational physics. By leveraging the power of neural networks, we can create more efficient, accurate, and user-friendly CFD simulations. As such approaches are widely explored and refined, I look forward to seeing their impact on the field of computational science and engineering.